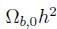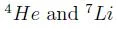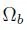Will New Russia is turning back to socialism? Victory Parade of 9th of May

The victory parade in Moscow on 9th of May is somewhat a chilling reminder of old soviet days. The parade comes after  the annexation of Crimea. 

Ok, we all know what Nikita Khrushchev did. After all he is the man who took out his shoe in UN while addressing the general assembly. He handed Crimea to Ukraine and after Putin's annexation of Crimea back to Russia,  Russian National pride is all time high.

 However this parade was quite similar to those conducted in the former USSR, which I used to watch since 1984. I was somewhat perplexed by this flag shown below behind the military vehicles.  It has hammer and sickle in it. And not only that. Flag on the left has CCCP printed on it, which is  USSR in Russian.

 Most interesting thing is the words used by the generals and soldiers. 

The Commanding General addressed the soldiers as comrade soldiers. Then the soldiers replied to him calling him "thovarish genaral" in Russian meaning comrade general. 

Then the General reported to Defence minister the readiness of the troops to the possession.  He addressed the minister as comrade minister and minister replied to him addressing as comrade general. 

Most intriguing part is that the minister addressed the  president putin as comrade Vladimir Putin and not as his excellency the president. 

Then Putin addressed the soldiers as  comrade soldiers. Is this normal? Or is it that Russia is firmly heading back to Soviet system with some sort of a mixed capitalist system like in China. In that case this day will be a memorable one. 

---ajith Dharmakeerthi 

Quantum tunnelling and Gamow Energy

Quantum tunnelling:

Quantum tunnelling also known as the barrier penetration, is the key to the occurrence of fusion reactions in stars. If the particle's total energy is less than the potential energy of some barrier it cannot pass that barrier. Think about throwing a ball over a wall. Unless there is sufficient kinetic energy to attain a height greater than the wall, there is no way the ball will reach the other side. Kinetic energy of the ball, once transformed to gravitational potential energy should exceed the gravitational potential energy of the wall.
However this restriction does not apply to quantum mechanics. We have to consider the wave properties of the particle in quantum mechanics. The amplitude of particle's wave function goes to zero only for an infinitely high barrier although the wave function associated with a particle is attenuated by a potential barrier.

As we know that the finite potential barriers exist in reality, the wave function inside and beyond the barrier is non-zero. Hence the position probability density is also non-zero. (position probability density).  Therefore there is a small but non-zero probability that a particle will make its way through a barrier, in such a case and even though that may appear impenetrable or insurmountable in normal circumstances. If we think about the ball again, if a ball and the wall were small enough for quantum properties to dominate over the classical scenario, it would be possible for a ball to reach the other side. That is even if it did not have enough kinetic energy to overcome the gravitational potential energy at the wall's top. This seems strange but this is precisely what happens during collisions of nuclei.

For the nucleus to be stable, the nucleons in a nucleus sit in a potential well surrounded by a Coulomb potential barrier of finite height and width. There is a non-zero probability of a particle with energy less than the height of the barrier would make its way from outside the barrier to inside due to barrier penetration to reach the nucleus.

The Gamow energy

The  barrier potentials do vary with separation, i.e. V is a function of r. For the Coulomb barrier, the penetration probability may be expressed in terms of the particle energy E, and the Gamow energy EG which depends on the atomic number of the interacting nuclei, and hence the size of the Coulomb barrier:

Therefor Gamow Energy:

where α is the fine structure constant ≈ 1/137.0.  and and C is Speed of light.
The rate of nuclear fusion therefore depends on the penetration probability of the Coulomb barrier. This penetration probability in turn is described by its Gamow energy.
A higher EG reduces the probability that the barrier will be penetrated. The Gamow energy measures the strength of the Coulomb repulsion, which determines the height of the Coulomb barrier.

The Gamow energy is named for George Gamow (1904–1968), a Russian physicist and cosmologist who escaped to the USA in 1934. His paper ‘The origin of chemical elements’ (1948) by Alpher, Bethe & Gamow attempted to explain much of astrophysical nucleosynthesis in the big bang and also predicted the existence of the cosmic microwave background radiation.

The Gamow Peak: 

The fusion probability as a function of energy for nuclei.  The energy at which the fusion rate is a maximum is called the Gamow peak. The region on either side of the peak in which the fusion probability is significant is called the Gamow window.

Ref: Stellar Evolution and Nucleosynthesis - Sean G Ryan, Andrew J Norton

Predicting the Abundances and Successes of the Standard Model

Predicting the Abundances: 
There are a few complications predicting the abundances. One of the complications is tracking the abundances of few dif ferent nuclei instead of just a single element hydrogen. Next problem is that neutrons are unstable when not in a nucleus. They have a half-life of about 11 minutes. Third, several light nuclei end products have very small binding energies, therefore delaying the freeze-out.

BBN has it's own shortcomings earlier on like not being able to produce the observed abundances of all of the element isotopes, primarily due to the unstable nuclei with atomic number A = 5 and A = 8. Therefore as Burbidge et al. (1957) correctly noted stellar nucleosynthesis caught attention of the astrophysicists. If we assumes that 4He is entirely of stellar origin, then we should be able to find places in the universe in which the 4He mass fraction 25% . The data for 4He ( The helium(Y) vs oxygen (O=H) abundances in extragalactic HII regions emphasized
the lack of low 4He regions. [ref: Olive (1999)] shows the fact that no such region with low 4He has been observed and that leads to a conclusion that BBN nucleosynthesis is responsible for 4He abundance and should be part of any cosmological model.

The element abundances depend on the number of baryons per photon, or on or  .
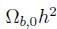
 Big Bang nucleosyntheis therefore makes very clear predictions for the
primordial abundances of elements created in the first half hour of the Universe's
existence. These predictions can be tested, and the overall level of agreement with
observations is one of the many successes of the Big Bang model. However, the
tricky part of the experiment is to determine primordial abundance of baryonic
matter that has remained in its primordial condition for the ~ 13.7 billion years
since the nucleosyntheis epoch.

Burles et al. (1999b) noted that, the predicted abundances of the light elements

 have been used to test the consistency of the hot big bang model at very early times (t ~0.01200sec). Fields et al. (1996) pointed out that the abundances of 4He and 7Li alone are su cient to probe and test the theory

and determine the single remaining parameter in the standard model, the baryon to
photon ratio.

Successes of the Standard Model

The assumptions that the standard model is based on are the laws of physics, which have been verifi ed at the present time by experiments, are also valid in the early universe. The cosmological principle described above holds. The temperature at early time t1 is greater than and contents of the universe are in thermal equilibrium.

It is suggested that (t1) is very close to 1. A baryon asymmetry is consistent with
observed radiation density.  It is assumed also that the initial density fluctuations gave rise to later formation of structures. The standard cosmology model nonetheless achieved success.

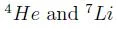
Close connections have been developed between theory and observations for Standard Big Bang Nucleosynthesis (SBBN), and observations are more and more reliable now. The BBN model leads to a deeper understanding of the creation of primordial elements and the predictions of the CMB. The most important of all is predicting abundances of   and explaining it through a single free parameter  .  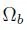The value of baryon density    agrees with other estimated values. 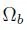Astrophysicists up to now used SBBN predictions and measured abundances to successfully estimate best values for cosmological parameters of baryon density  and baryon to photon ratio   . Generally one uses the low D/H ratio as the decent estimator for find for the baryon density. The next chapter will show that, the observed abundances of elements D, 4He and 7Li are close to the primordial abundances predicted by SBBN.

References:
1.E. M. Burbidge, G. R. Burbidge, W. A. Fowler, and F. Hoyle. Synthesis of
the elements in stars. Rev. Mod. Phys., 29:547{650, Oct 1957. doi: 10.1103/
RevModPhys.29.547. URL http://link.aps.org/doi/10.1103/RevModPhys.
29.547.
2. S. Burles, K. M. Nollett, J. W. Truran, and M. S. Turner. Sharpening the predictions of big-bang nucleosynthesis. Physical Review Letters, 82:4176{4179, May 1999b. doi: 10.1103/PhysRevLett.82.4176.
3. B. D. Fields, K. Kainulainen, K. A. Olive, and D. Thomas. Model independent
predictions of big bang nucleosynthesis from ^4He and ^7Li: consistency and
implications. New A, 1:77{96, July 1996. doi: 10.1016/S1384-1076(96)00007-3.